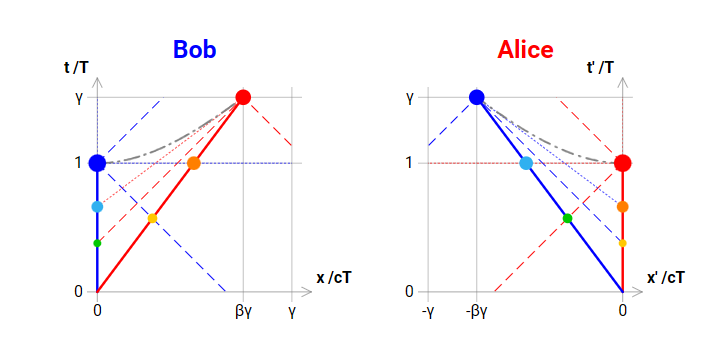
Bob and Alice pass by each other collinearly at a relative constant speed.
They reset their clocks to zero at the moment they are colocated.
Go to interactive diagram
Go back to project page

In either frame of reference, we compute coordinates and velocities of:
The space-time diagrams make concrete the clock hypothesis, i.e. proper time as absolute time, recovering absolute time as the fundamental dynamic variable, and with it the relativistic symmetry of the frame perspectives.
The diagrams also show that, relative to any frame of reference, any particle moves into the future and in space at a speed that is faster than measured in that frame (i.e. in a plane of simultaneity) by exactly its Lorentz factor. And this already and essentially is time travel.
In particular, the 4-velocity of light in any frame of reference is (scalarly) infinite in all components, its magnitude being exactly the measured light speed times its Lorentz factor (see below for the formal details).
In Special Relativity in $1\+1$ dimensions,
with generic coordinates $\ovP \~ \vec{t^\vex{\P}}{x^\vex{\P}}\!$,
and velocities $\ovv^\vex{\P} \~ \vec{v_t^\vex{\P}}{v_x^\vex{\P}}\!$.
Given $\c \ino{0}{\infty}$ the measured speed of light.
Given $\T \ino{0}{\infty}$ the proper time period.
For $v \inc{0}{1}\c$ a (constant) measured frame speed
(i.e., WLOG, we are only considering the case
$v\ge\!0$ in the unprimed frame).
For $\t \inc{0}{1}\T$ a proper time (by the clock).
Let $\b \= \b\!_v \is v\/\c \inc{0}{1}\!$.
Let $\gb \is 1/{\small \sqr{1\-\b^2}} \inc{1}{\gc}\!$.
Let $\epb \is 1/{\small (1\+\b)} \inc{1/2}{1}\!$.
Let $\enb \is 1/{\small (1\-\b)} \inc{1}{2\,\gc^2}\!$.
where $\epb\;\enb \= \gb^2$.
(Note that, instead of saying $\gb \inc{1}{\infty}$, which is undefined,
we keep track of $\gb$ throughout as a scale factor, so we can keep our
intervals closed and have a uniform and finitely representable treatment
for all $v$. In fact, we make explicit the range of all coordinates to
facilitate delimiting the space-time diagrams.)
Diagramatically, for any fixed velocity $\uhat{v}$ and point $\uhat{\ovP} \~ \vec{\uhat{t}}{\uhat{x}}$:
Finally, for reference, the form of our Lorentz transformations is:
$\pri{t} \= \gb\, (t \- \v x/\c^2)$
$\pri{x} \= \gb\, (x \- \v t)$
We parametrize all formulas, besides implicitly on the (measured) relative speed, on the one and only (universal) proper time.
This is the frame of reference in which Bob is at rest at the origin of space.
We derive coordinates in this frame, whence velocities, by imposing the relevant physical constraints, then by plain geometry.
This represents Bob's actual space-time position.
We derive coordinates of $\BBa$ in this frame by imposing the constraints that Bob is at rest at the origin of space, hence $x \= 0$, and that Bob's proper distance from the origin of space-time is $|\t|$, hence by the metric $|\t| \= {\small \sqr{{t}^2 \- x^2/\c^2}} \= {\small \sqr{{t}^2}} \= |t|$, whence, with the direction of $t$ in accordance with that of $\t$, $t \= \t$.
In summary, we get:
$\pBBa(\t) \~ \vec{1}{0}\t$
$\ovv^\vex{\BBa}(\t) \~ \vec{1}{0}$
with coordinates as derived above:
$t^\vex{\BBa}(\t) \= \t \quad\, \inc{0}{1}\T \;\;\; \subseteq \ivc{0}{1}\T$
$x^\vex{\BBa}(\t) \= 0 \quad \inc{0}{0}\c\T \; \subseteq \ivc{0}{0}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
Also, since Bob's measured speed is $0 \= x^\vex{\BBa} / t^\vex{\BBa}$:
This represents Alice's actual space-time position.
We derive coordinates of $\BAa$ in this frame by imposing the constraints that Alice's measured speed is $v$, hence $x \= \v t$, and that Alice's proper distance from the origin of space-time is $|\t|$, hence by the metric $|\t| \= {\small \sqr{{t}^2 \- x^2/\c^2}} \= {\small \sqr{{t}^2 \- v^2\,t^2/\c^2}} \= |t|\/\gb$, whence, with the direction of $t$ in accordance with that of $\t$, $t \= \gbt$ and $x \= \v\gbt$.
In summary, we get:
$\pBAa(\t) \~ \vec{1}{v}\gbt$
$\ovv^\vex{\BAa}(\t) \~ \vec{1}{v}\gb$
with coordinates as derived above:
$t^\vex{\BAa}(\t) \= \gbt \quad\quad \inc{0}{\gb}\T \quad\;\; \subseteq \ivc{0}{\gb}\T$
$x^\vex{\BAa}(\t) \= \v\gbt \quad\, \inc{0}{\b\gb}\c\T \; \subseteq \ivc{0}{\gb}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
Also, since Alice's measured speed is $v \= x^\vex{\BAa} / t^\vex{\BAa}$:
This represents what Bob measures of Alice: here he finds her time-dilated and length-contracted.
We derive coordinates of $\BAs$ in this frame by intersecting Alice's world line, $t \= x\/v$, with Bob's simultaneity plane, $t \= \t$, whence $x \= \v\t$.
In summary, we get:
$\pBAs(\t) \~ \vec{1}{v}\t$
$\ovv^\vex{\BAs}(\t) \~ \vec{1}{v}$
with coordinates as derived above:
$t^\vex{\BAs}(\t) \= \t \quad\quad \inc{0}{1}\T \quad\, \subseteq \ivc{0}{1}\T$
$x^\vex{\BAs}(\t) \= \v\t \quad\; \inc{0}{\b}\c\T \; \subseteq \ivc{0}{1}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
This represents what Alice measures of Bob: here she finds him time-dilated and length-contracted.
We derive coordinates of $\BBs$ in this frame by intersecting Bob's world line, $x \= 0$, with Alice's simultaneity plane, $t \= \t/\gb \+ \b x/\c$, whence $t \= \t/\gb$.
In summary, we get:
$\pBBs(\t) \~ \vec{1}{0}\t/\gb$
$\ovv^\vex{\BBs}(\t) \~ \vec{1}{0}/\gb$
with coordinates as derived above:
$t^\vex{\BBs}(\t) \= \t/\gb \quad \inc{0}{1/\gb}\T \; \subseteq \ivc{0}{1/\gb}\T$
$x^\vex{\BBs}(\t) \= 0 \quad\quad\; \inc{0}{0}\c\T \quad\, \subseteq \ivc{0}{0}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
This represents what to Bob appears of Alice, i.e. by just observing her from his position.
We derive coordinates of $\BAv$ in this frame by intersecting Alice's world line, $t \= x\/v$, with Bob's negative light cone, $t \= \t \- x/\c$, whence $t \= \epb\t$ and $x \= \v\epb\t$.
In summary, we get:
$\pBAv(\t) \~ \vec{1}{v}\epb\t$
$\ovv^\vex{\BAv}(\t) \~ \vec{1}{v}\epb$
with coordinates as derived above:
$t^\vex{\BAv}(\t) \= \epb\t \quad\quad \inc{0}{\epb}\T \quad\;\; \subseteq \ivc{0}{1}\T$
$x^\vex{\BAv}(\t) \= \v\epb\t \quad\, \inc{0}{\b\epb}\c\T \; \subseteq \ivc{0}{1/2}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
This represents what to Alice appears of Bob, i.e. by just observing him from her position.
We derive coordinates of $\BBv$ in this frame by intersecting Bob's world line, $x \= 0$, with Alice's positive light cone, $t \= \epb\t/\gb \+ x/\c$, whence $t \= \epb\t/\gb$.
In summary, we get:
$\pBBv(\t) \~ \vec{1}{0}\epb\t/\gb$
$\ovv^\vex{\BBv}(\t) \~ \vec{1}{0}\epb\/\gb$
with coordinates as derived above:
$t^\vex{\BBv}(\t) \= \epb\t/\gb \quad \inc{0}{\epb\/\gb}\T \; \subseteq \ivc{0}{1}\T$
$x^\vex{\BBv}(\t) \= 0 \quad\quad\quad\;\, \inc{0}{0}\c\T \quad\quad \subseteq \ivc{0}{0}\c\T$
whence, by taking derivatives w.r.t. $\t$, the velocity.
Extrapolating, coordinate boundaries in frame $\B$ are:
$t \in \ivc{0}{\gb}\T \quad\;\;\, \subseteq \ivc{0}{\gb}\T$
$x \in \ivc{0}{\b\gb}\c\T \; \subseteq \ivc{0}{\gb}\c\T$
This is the frame of reference in which Alice is at rest at the origin of space.
We derive coordinates in this frame by Lorentz-transforming by speed $v$ the corresponding coordinates in frame $\B$.
We double-check that the results obtained are symmetric to those in frame $\B$, i.e. they are the same modulo swapping any $\pri{\A}$, resp. $\pri{\B}$ particles with the corresponding $\B$, resp. $\A$ particles, and inverting the sign of the space coordinates in all places.
Given that $\pBAa(\t) \~ \vec{1}{v}\gbt$, by transforming coordinates we get:
$\pri{t}^\vex{\AAa}(\t) \= \gb \left( \gbt \- v^2\,\gbt/\c^2 \right) \= \t$
$\pri{x}^\vex{\AAa}(\t) \= \gb \left( \v\gbt \- \v\gbt \right) \= 0$
Whence $\pAAa(\t) \~ \vec{1}{0}\t$, symmetric to $\pBBa$ as expected.
Given that $\pBBa(\t) \~ \vec{1}{0}\t$, by transforming coordinates we get:
$\pri{t}^\vex{\ABa}(\t) \= \gb \left( \t \- 0 \right) \= \gbt$
$\pri{x}^\vex{\ABa}(\t) \= \gb \left( 0 \- \v\t \right) \= \!-\!\!\v\gbt$
Whence $\pABa(\t) \~ \vec{1}{-\!v}\gbt$, symmetric to $\pBAa$ as expected.
Given that $\pBBs(\t) \~ \vec{1}{0}\t/\gb$, by transforming coordinates we get:
$\pri{t}^\vex{\ABs}(\t) \= \gb \left( \t/\gb \- 0 \right) \= \t$
$\pri{x}^\vex{\ABs}(\t) \= \gb \left( 0 \- \v\t/\gb \right) \= \!-\!\!\v\t$
Whence $\pABs(\t) \~ \vec{1}{-\!v}\t$, symmetric to $\pBAs$ as expected.
Given that $\pBAs(\t) \~ \vec{1}{v}\t$, by transforming coordinates we get:
$\pri{t}^\vex{\ABa}(\t) \= \gb \left( \t \- v^2\,\t/\c^2 \right) \= \t/\gb$
$\pri{x}^\vex{\ABa}(\t) \= \gb \left( \v\t \- \v\t \right) \= 0$
Whence $\pAAs(\t) \~ \vec{1}{0}\t/\gb$, symmetric to $\pBBs$ as expected.
Given that $\pBBv(\t) \~ \vec{1}{0}\epb\t/\gb$, by transforming coordinates we get:
$\pri{t}^\vex{\ABa}(\t) \= \gb \left( \epb\t/\gb \- 0 \right) \= \epb\t$
$\pri{x}^\vex{\ABa}(\t) \= \gb \left( 0 \- \v\epb\t/\gb \right) \= \!-\!\!\v\epb\t$
Whence $\pABv(\t) \~ \vec{1}{-\!v}\epb\t$, symmetric to $\pBAv$ as expected.
Given that $\pBAv(\t) \~ \vec{1}{v}\epb\t$, by transforming coordinates we get:
$\pri{t}^\vex{\ABa}(\t) \= \gb \left( \epb\t \- v^2\,\epb\t/\c^2 \right) \= \epb\t/\gb$
$\pri{x}^\vex{\ABa}(\t) \= \gb \left( \v\epb\t \- \v\epb\t \right) \= 0$
Whence $\pAAv(\t) \~ \vec{1}{0}\epb\t/\gb$, symmetric to $\pBBv$ as expected.
Symmetrically to frame $\B$, coordinate boundaries in frame $\A$ are:
$\pri{t} \in \ivc{0}{\gb}\T \quad\quad\:\, \subseteq \ivc{0}{\gb}\T$
$\pri{x} \in \ivc{-\!\b\gb}{0}\c\T \; \subseteq \ivc{-\!\gb}{0}\c\T$
That completes our calculations.
SR/InertialFrames v2.2.2
© 2020-2025 Julio P. Di Egidio
Released under GNU-GPLv3
Project home page